- Зохиолч admin carl@lifeloveeveryday.com.
- Public 2023-12-16 19:25.
- Хамгийн сүүлд өөрчлөгдсөн 2025-01-23 15:32.

Алтан харьцааны жишээг сонгодог архитектур, урлагийн бүтээл, байгаль, тэр ч байтугай хөгжимөөс хаанаас ч олж болно. Тэнгэрлэг харьцаа гэгддэг энэхүү пропорцын илэрхийлэл нь байгалийн болон хүний гараар бүтээгдсэн загварт иррационал тоог (1.618) хэрэглэснээр зохицолтой найрлагыг санал болгодог. Алтан харьцаа нь ямар ч тайлбар шаардлагагүйгээр аяндаа таалагдах объект, хөгжмийг бүтээдэг учраас та математикийн гоо сайхныг мэдэхгүй байх магадлалтай.
Архитектур дахь Алтан харьцаа
Алтан харьцаа нь байгаль, урлагт бараг төгс гоо сайхныг бий болгодог. Алтан харьцааны жишээг өдөр тутмын амьдралдаа хайж эхлэхэд олон дурсгалт барилга, байгууламжийг бий болгоход ашигласан олон тохиолдлууд таныг гайхшруулж магадгүй юм. Архитектурт "Алтан харьцаа" -г ашиглах үед уг барилгыг "ариун архитектур" -ыг ашиглан бүтээсэн гэж үздэг. Алтан харьцааны тооцоог квадратад хэрэглэснээр архитекторууд болон дизайнерууд хүний нүдэнд гоо зүйн хувьд хамгийн тааламжтай харьцаатай гэж үздэг Алтан тэгш өнцөгтийг бүтээх боломжтой.
Алтан тэгш өнцөгт Жишээ: Парфенон

Грекийн уран барималч Фидиас бүтээлдээ Алтан харьцааг ашигласан, ялангуяа Парфеноны баганын яг дээгүүр сийлсэн хамтлагуудтай ажиллаж эхлэхдээ. Мөн Алтан харьцаанд өгсөн тоон утгыг Фи гэж нэрлэсэн гэдгийг тэмдэглэх нь зүйтэй.
Хэрэв та Парфеноны гадна талын хэмжээсийг хэмжиж үзвэл энэ нь зөвхөн Алтан тэгш өнцөгтийг үүсгээд зогсохгүй, баганын хооронд олон Алтан тэгш өнцөгт байгааг олж мэдэх болно. Энэхүү ариун дагшин байгууламж нь архитектур дахь Алтан харьцааны сайхан жишээ юм.
Алтан гурвалжин Жишээ: Гизагийн агуу пирамид
Алтан харьцаа, Алтан тэгш өнцөгт, Алтан гурвалжин зэргийг дэлхийн долоон гайхамшгийн нэг болох Гизагийн агуу пирамидаас олж болно. Алтан харьцааг олохын тулд та пирамидын дөрвөлжин суурийг хоёр дахин багасгаж, пирамидын төв рүү босоо шугам зурах хэрэгтэй. Үүнийг пирамидын өнцгийн талтай холбосноор Алтан харьцаа буюу 1.618 харьцаатай Алтан гурвалжинг хэрхэн үүсгэхийг хялбархан харж болно.
Архитектурын бусад жишээнүүд
Та эртний болон орчин үеийн ариун архитектур, Алтан харьцаатай барилгуудын олон жишээг олж болно.
- Chartres Cathedral - Төв, Франц
- Нотр Дам - Франц, Парис
- Охидын үүдний танхим - Акрополис, Афин
- Таж Махал - Агра, Энэтхэг
- Нэгдсэн Үндэстний Байгууллагын байр - Нью Йорк хот, Нью Йорк
Урлагийн жишээн дэх алтан харьцаа
Алтан харьцааг ашигласан мастер зураачдын олон жишээг та олж болно. Алтан тэгш өнцөгт ба алтан гурвалжны харьцааг ашиглан эдгээр төгс бүтээлүүдийг бүтээсэн. Алтан тэгш өнцөгт дээр тулгуурлан бүтээсэн урлаг нь хүний нүдэнд илүү тааламжтай байдаг. Энэ бол төгс тэгш өнцөгт ба Алтан харьцааг тойрсон нууцуудын нэг юм.
Урлагт алтан харьцаа

Алтан харьцааны урлагийн жишээнд:
- Леонардо Ди Винчи - Мона Лиза, Витрувийн хүн
- Боттичелли - Сугар гараг
- Микеланджело - Ариун гэр бүл, 'Дэвид'
- Рафаэл - Цовдлолт
- Рембрандт - Өөрийгөө хөрөг
- Сальвадор Дали - Сүүлчийн зоогийн ариун ёслол, Санах ойн тууштай байдал
Уран сайхны найруулгад алтан харьцааг ашиглах нь
Алтан тэгш өнцөгт дотор бусад хэсгүүдээс илүү харагдахуйц харагддаг зарим хэсгүүд байдаг. Эдгээр цэгүүдийг тэгш өнцөгтийн доод булангаас эсрэг талын өнцөг хүртэл зурж, нөгөө доод булангаар давтах замаар илрүүлдэг. Эдгээр шугамууд нь Алтан тэгш өнцөгтийн яг төвд огтлолцоно. Дараа нь төв цэгээс эхлэн шугам бүрийн дагуу дунд хэсгийг хэмжинэ. Эдгээр дөрвөн цэгийг тэгш өнцөгтийн нүд (Алтан харьцаа) гэж нэрлэдэг. Дараа нь зургийн гол гол цэгийг эдгээр сонирхлын цэгүүдэд (харьцаа) зурж эсвэл зурдаг.
Хөгжмийн алтан харьцаа

Хөгжим нь тоон утгаас тогтдог бөгөөд Алтан харьцаагаар хөгжмийн зохиол бүтээхэд математикийн амьд жишээ болдог. Фибоначчийн дараалал нь хөгжимд бас түгээмэл байдаг:
- Маскаарт найман тэмдэглэл байна.
- Гурав, тав дахь нот нь хөвчний үндэс болдог.
- Аливаа ноотын урт буюу октав нь 13 нот байна.
Дараалал нь хөгжмийн зохиолын туршид үргэлжилж, Алтан харьцаанд хүрэх тусам илүү төвөгтэй болдог.
Алтан харьцаа ашигласан хөгжмийн зохиолчид
Хамгийн алдартай сонгодог хөгжмийн зохиолчдын зарим нь Бах, Бетховен, Шопен, Моцарт зэрэг хөгжмийн зохиолдоо Алтан харьцаа, Фибоначчийн дарааллыг ашигласан байдаг. Кейси Монговен зэрэг орчин үеийн зарим хөгжмийн зохиолчид өөрсдийн хөгжимдөө Алтан харьцааг судалсан байдаг.
Байгалийн алтан харьцааны жишээ

Алтан харьцаа байгальд хаана байдаг вэ? Энэ нь Алтан харьцааг ашиглан үүсгэж болох Алтан эсвэл Фибоначчийн спиральд байдаг. Энэ бол байгалийн ертөнцөд өргөн тархсан үзэгдэл юм. Ургамлын навчнууд нь ишийг нь эргүүлж чадахуйц их хэмжээгээр ургадаг. Шинэ навч үүссэний дараа л үүснэ.
- Спираль какти
- Спираль галактикууд
- Наранцэцэг
Фибоначчийн дараалалтай цэцэг
Зарим цэцэг Фибоначчийн дарааллыг дагасан цэцгийн дэлбээтэй байдаг:
- Гурван дэлбээ:Цахилдаг, сараана, цахирмаа, триллиум
- Таван дэлбээ: Царцган цэцэг, шит цэцэг, хибискус, өглөөний алдар, настуртиум
- Найман дэлбээтэй: Delphiniums
- 13 дэлбээтэй: Зарим төрлийн дацис, ноорхой, мариголд
Нарсны боргоцой дахь Фибоначчийн спираль

Модны төрлөөс хамааран та нарс боргоцой дахь Фибоначчийн тооны цуврал доторх Алтан харьцааг харж болно. Нарсны боргоцойны нэг тал дээр 13 спиральтай, нөгөө талд нь найман спираль цуваа олж болно. Өөр нэг нарс модны хээ нь нэг талдаа наймтай, нөгөө талдаа таван спиральтай.
Хүний алтан харьцаа
Энэ харьцаа нь зөвхөн хүмүүс бие биенээ хэрхэн хардаг төдийгүй тэдний бие хэрхэн ажилладаг, ДНХ-д ч чухал юм.
ДНХ Алтан харьцааг илчилж байна
Алтан харьцааны хамгийн гайхалтай жишээнүүдийн нэг нь хүний ДНХ-ийн бүтцэд байдаг. Үүнийг нэг ДНХ-ийн хөндлөн огтлолоос харж болно, ДНХ-ийн давхар мушгиа нь арван өнцөгт хэлбэртэй байдаг. Энэ нь бие биенээсээ 36 градус эргүүлсэн хоёр таван өнцөгтийн хослол бөгөөд ДНХ-ийн давхар мушгиа үүсгэдэг. Давхар мушгиа спираль нь өөрөө таван өнцөгт үүсгэдэг. Ганц ДНХ молекул ч гэсэн Алтан хэсэг буюу Тэнгэрлэг харьцааны үндсийг илчилдэг.
Алтан харьцааны цаад математик
Алтан харьцааг бодит амьдрал дээр олох нь таны эргэн тойронд харагддаг тул энгийн зүйл юм. Энэ нь олон зуун жилийн турш хүн төрөлхтний хуулбарлаж, дуурайлган байгалиас олдсон төгс тоо гэгддэг математикийн үнэн зөвийг тодорхойлоход ашигладаг. Энэ тооны энгийн гоо үзэсгэлэн нь гүйцэтгэлийн нарийн төвөгтэй байдлыг далдалдаг. Алтан харьцааны онолыг ойлгохын тулд эхлээд Фибоначчийн харьцааны дарааллыг судлах хэрэгтэй.
Фибоначчийн дараалал ба алтан харьцаа
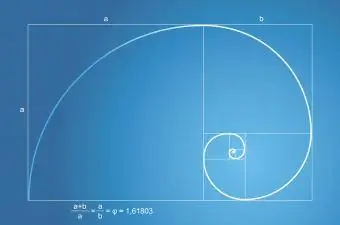
Фибоначчийн дараалал буюу цуврал нь Алтан харьцаатай холбоотой. Фибоначчийн цуврал нь ургамлын навчны тоо, цэцэг дээрх дэлбээний тоогоор илэрдэг. Байгальд байдаг Фибоначчийн спираль нь үргэлж алтан харьцаатай Алтан тэгш өнцөгтийн нэг хэсэг юм.
Фибоначчийн цувралын математик энгийн:
- Дараалал 0 ба 1-ээр эхэлдэг.
- Сүүлийн хоёр тоог нэмээд цувралын дараагийн дугаарыг аваарай.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8 гэх мэт.
- Энэ Фибоначчийн цувралын жишээ нь: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 гэх мэт.
Фибоначчийн Алтан харьцааг урагш, цааш, цааш нь нэмбэл ойлгодог. Цуврал нэмэх тусам Алтан харьцаанд ойртох болно.
Алтан тэгш өнцөгт гурвалжин үүсгэх
Фибоначчийн дарааллаар Алтан тэгш өнцөгт үүсгэхийн тулд та квадратаас эхэлнэ. Та анхны дөрвөлжин дээрээ өөр дөрвөлжин нэмж тэгш өнцөгт барьж эхэлнэ. Томъёог ашиглахаа мартуузай: 0+1=1 нь эхний квадрат, 1+1=2 - та өөр квадрат нэмнэ.1+2=3 бол гурван квадрат, дараагийнх нь 2+3=5 бол таван квадрат нэмнэ. Та үргэлжлүүлэн квадрат нэмж, эцэст нь Алтан тэгш өнцөгт үүсгэх болно.
Алтан тэгш өнцөгтийг нэг булангаас эсрэг талын өнцөг хүртэл хоёр хуваасан байдлаар Алтан гурвалжин үүсгэж болно. Ингэснээр түүний гурван тал буюу өнцөг нь 2:2:1 харьцаатай гурвалжин үүснэ. Энэ нь хоёр урт талын урт нь тэнцүү, богино өнцөг нь хоёр урт талынхаас яг хагасын урттай тэнцүү байна.
Бодит ертөнц дэх алтан харьцаа
Алтан харьцаа нь байгаль болон хүний биед онцгой байр суурь эзэлдэг тул ихэвчлэн Тэнгэрлэг харьцаа гэж нэрлэдэг. Алтан харьцаа нь маш олон амьд биетэд агуулагддаг болохыг олж мэдсэн нь энэхүү ид шидийн хувь хэмжээг хүндэтгэх сэтгэлийг төрүүлсэн бөгөөд энэ нь одоо ч уран бүтээлчид болон бүтээгчдэд урам зориг өгсөн хэвээр байна.






